在正方体ABCD-A1B1C1D1中，E、F分别是CD、A1D1中点．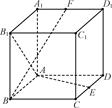
(1)求证：AB1⊥BF；
(2)求证：AE⊥BF；
(3)棱CC1上是否存在点F，使BF⊥平面AEP，若存在，确定点P的位置；若不存在，说明理由．
相关试题
的各项均为正数，观察程序框图，若
时，分别有
．
，求数列
的前
项和
．
中，
分别是
，
的中点。
平面
；
，求异面直线
与
所成角的大小．（本小题满分12分）已知
,
,
且函数
（1）设方程
在
内有两个零点
，求
的值；
（2）若把函数
的图像向左平移
个单位,再向上平移2个单位,得函数
图像,求函数在
上的单调增区间．
在
上单调递增，函数
的值；
时，记
的值域分别为
，若
，求实数
的取值范围．
．
的单调区间；
是否存在极值，若存在，请求出极值；若不存在，请说明理由；
时．证明：
．推荐套卷
在正方体ABCD-A1B1C1D1中，E、F分别是CD、A1D1中点．
(1)求证：AB1⊥BF；
(2)求证：AE⊥BF；
(3)棱CC1上是否存在点F，使BF⊥平面AEP，若存在，确定点P的位置；若不存在，说明理由．
（本小题满分12分）已知,,
且函数
（1）设方程在内有两个零点，求的值；
（2）若把函数的图像向左平移个单位,再向上平移2个单位,得函数图像,求函数在上的单调增区间．
粤公网安备 44130202000953号