如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).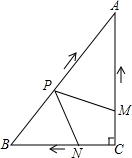
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
相关知识点
推荐套卷
 (
( ≠0)与
≠0)与 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与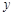 轴交与点C(0,2).
轴交与点C(0,2).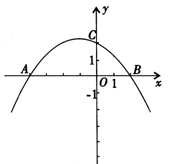
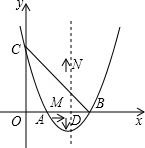
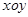 中,抛物线
中,抛物线 与
与 轴交于
轴交于 ,与y轴交于
,与y轴交于 ,顶点为
,顶点为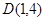 ,对称轴为
,对称轴为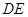 .
. 是
是 上的一个动点,
上的一个动点, 是
是 ,过
,过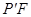 ∥
∥ .设
.设 ,求
,求 关于
关于 ,使
,使 成为以
成为以 为直角边的直角三角形?若存在,求出
为直角边的直角三角形?若存在,求出
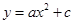 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.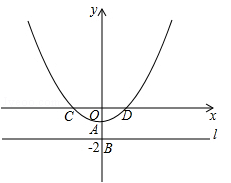

 粤公网安备 44130202000953号
粤公网安备 44130202000953号