已知双曲线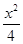
-
=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.
(1)求b的值;
(2)抛物线y2=2px(p>0)的焦点与该双曲线的右顶点重合,斜率为1的直线经过右顶点,与该抛物线交于A、B两点,求弦长|AB|.
相关试题
，离心率
，且过点
，
以
为直角顶点，边
与椭圆交于
两点，求
面积的最大值．
平面
,
为等边三角形，
平面
，求CD长度；
中，角A,B,C所对的边分别为a,b,c, 已知a,b,c成等比数列，且
．
，求
求
的单调区间；
＞1时，求
上的最小值；
若
使得
成立，求
的范围．
的焦点
以及椭圆
的上、下焦点及左、右顶点均在圆
上．
和椭圆
的标准方程；
的直线交抛物线
、
两不同点,交
轴于点
，已知
为定值．相关知识点
推荐套卷
已知双曲线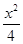-=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.
(1)求b的值;
(2)抛物线y2=2px(p>0)的焦点与该双曲线的右顶点重合,斜率为1的直线经过右顶点,与该抛物线交于A、B两点,求弦长|AB|.
粤公网安备 44130202000953号