已知数列{an}满足a1＋a2＋…＋an＝n2(n∈N*)．
(1)求数列{an}的通项公式；
(2)对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使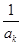
，
，
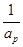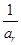成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
，且
，
的值；
，
，求
．
的值．
的值．
中，以
轴为始边作两个锐角
，它们的终边分别交单位圆于
两点．已知
，
．
的值；
的值．
，
；（2）
的值
的值；
是第三象限的角，化简三角式
，并求值．相关知识点
推荐套卷
已知数列{an}满足a1＋a2＋…＋an＝n2(n∈N*)．
(1)求数列{an}的通项公式；
(2)对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使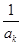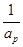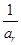，，成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
粤公网安备 44130202000953号