已知各项均为正数的等比数列{an}的公比为q，且0＜q＜
.
(1)在数列{an}中是否存在三项，使其成等差数列？说明理由；
(2)若a1＝1，且对任意正整数k，ak－(ak＋1＋ak＋2)仍是该数列中的某一项．
(ⅰ)求公比q；
(ⅱ)若bn＝－logan＋1(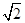
＋1)，Sn＝b1＋b2＋…＋bn，Tr＝S1＋S2＋…＋Sn，试用S2011表示T2011.
相关试题
,
的最小正周期，并求
上的最小值；
中，
分别是角
的对边，
为锐角，若
，
，
，求
.
,
的单调区间；
上的最值.
,
的值；
，求
.
R，函数
e
．
没有零点，求实数
的取值范围；
，求
时，求证：
．
的表达式；推荐套卷
已知各项均为正数的等比数列{an}的公比为q，且0＜q＜.
(1)在数列{an}中是否存在三项，使其成等差数列？说明理由；
(2)若a1＝1，且对任意正整数k，ak－(ak＋1＋ak＋2)仍是该数列中的某一项．
(ⅰ)求公比q；
(ⅱ)若bn＝－logan＋1(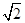＋1)，Sn＝b1＋b2＋…＋bn，Tr＝S1＋S2＋…＋Sn，试用S2011表示T2011.
粤公网安备 44130202000953号