已知数列的前n项和为Sn，并且满足a1＝2，nan＋1＝Sn＋n(n＋1)．
(1)求{an}的通项公式；
(2)令Tn＝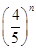
Sn，是否存在正整数m，对一切正整数n，总有Tn≤Tm？若存在，求m的值；若不存在，说明理由．
=
,M
=
,求M2.
=
M
成立的矩阵M.
,B=
,C=
,求AB和AC.
的逆矩阵.相关知识点
推荐套卷
已知数列的前n项和为Sn，并且满足a1＝2，nan＋1＝Sn＋n(n＋1)．
(1)求{an}的通项公式；
(2)令Tn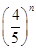＝ Sn，是否存在正整数m，对一切正整数n，总有Tn≤Tm？若存在，求m的值；若不存在，说明理由．
粤公网安备 44130202000953号