已知数列{an}的前n项和Sn与通项an满足Sn=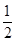 -
-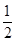 an.
an.
(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=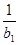 +
+ +…+
+…+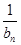 ,求T2012;
,求T2012;
(3)若cn=an·f(an),求{cn}的前n项和Un.
相关知识点
推荐套卷
已知数列{an}的前n项和Sn与通项an满足Sn=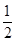 -
-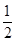 an.
an.
(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=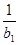 +
+ +…+
+…+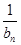 ,求T2012;
,求T2012;
(3)若cn=an·f(an),求{cn}的前n项和Un.