如图所示,三棱柱ABC
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
AB.
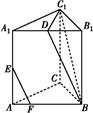
(1)求证:EF∥平面BC1D;
(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1∶15,若存在,指出点G的位置;若不存在,说明理由.
相关试题
+cos
,
的值 (2)求
的值.
中，已知
，
，试判断
在R上为奇函数,
，
.
的值;
的单调性.（不需要证明）
,都有
;是否存在
的值，使
最小值为
；
满足
，
;数列
满足
，
和
的通项公式
的前
项和
相关知识点
推荐套卷
如图所示,三棱柱ABCA1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=AB.
(1)求证:EF∥平面BC1D;
(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1∶15,若存在,指出点G的位置;若不存在,说明理由.
粤公网安备 44130202000953号