要制作一个如图的框架(单位：m)，要求所围成的总面积为19.5(m2)，其中ABCD是一个矩形，EFCD是一个等腰梯形，梯形高h＝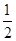
AB，tan∠FED＝
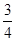，设AB＝xm，BC＝ym.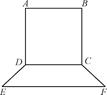
(1)求y关于x的表达式；
(2)如何设计x、y的长度，才能使所用材料最少？
，
，求
的值。
求
的值。
。
中，若已知三边为连续正整数，最大角为钝角，
中，求证：
．推荐套卷
要制作一个如图的框架(单位：m)，要求所围成的总面积为19.5(m2)，其中ABCD是一个矩形，EFCD是一个等腰梯形，梯形高h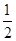＝AB，tan∠FED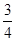＝，设AB＝xm，BC＝ym.
(1)求y关于x的表达式；
(2)如何设计x、y的长度，才能使所用材料最少？
粤公网安备 44130202000953号