如图，ABCD是正方形空地，边长为30m，电源在点P处，点P到边AD、AB距离分别为9m、3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF，MN∶NE＝16∶9.线段MN必须过点P，端点M、N分别在边AD、AB上，设AN＝x(m)，液晶广告屏幕MNEF的面积为S(m2)．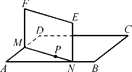
(1)用x的代数式表示AM；
(2)求S关于x的函数关系式及该函数的定义域；
(3)当x取何值时，液晶广告屏幕MNEF的面积S最小？
中，
，求
，并归纳出
.
中，
，求
的值.
，其中后一项比前一项大2.
是否为此数列的项？
中，
，求
，并归纳出
.
的前
项和
，分别求它们的通项公式
.
；⑵
.推荐套卷
如图，ABCD是正方形空地，边长为30m，电源在点P处，点P到边AD、AB距离分别为9m、3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF，MN∶NE＝16∶9.线段MN必须过点P，端点M、N分别在边AD、AB上，设AN＝x(m)，液晶广告屏幕MNEF的面积为S(m2)．
(1)用x的代数式表示AM；
(2)求S关于x的函数关系式及该函数的定义域；
(3)当x取何值时，液晶广告屏幕MNEF的面积S最小？
粤公网安备 44130202000953号