.(本小题满分12分)
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:
①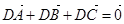 ;②|
;②| |=
|=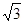 |
|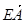 |=
|=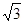 |
|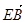 |③
|③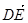 与
与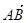 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ) 若斜率为1直线l与动点C的轨迹交于M,N两点,且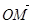 ·
·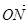 =0,求直线l的方程.
=0,求直线l的方程.
推荐套卷
.(本小题满分12分)
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:
①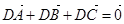 ;②|
;②| |=
|=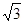 |
|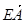 |=
|=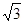 |
|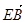 |③
|③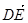 与
与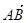 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ) 若斜率为1直线l与动点C的轨迹交于M,N两点,且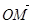 ·
·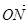 =0,求直线l的方程.
=0,求直线l的方程.