已知函数f(x)＝lnx，g(x)＝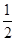
ax2＋bx(a≠0)，设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q，过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N，问是否存在点R，使C1在点M处的切线与C2在点N处的切线互相平行？若存在，求出点R的横坐标；若不存在，请说明理由．
相关试题
求
的值．
的定义域、值域和单调区间．相关知识点
推荐套卷
已知函数f(x)＝lnx，g(x)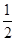＝ax2＋bx(a≠0)，设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q，过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N，问是否存在点R，使C1在点M处的切线与C2在点N处的切线互相平行？若存在，求出点R的横坐标；若不存在，请说明理由．
粤公网安备 44130202000953号