如图，线段AB，CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1（升）、y2（升）关于行驶时间x（小时）的函数图象．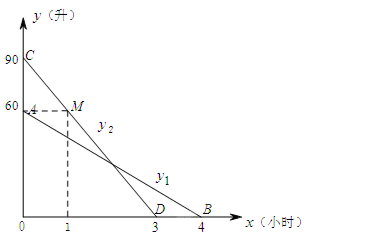
（1）分别求y1、y2关于x的函数解析式，并写出定义域；
（2）如果两车同时从相距300千米的甲、乙两地出发，相向而行，匀速行驶，已知轿车的行驶速度比客车的行驶速度快30千米/小时，且当两车在途中相遇时，它们油箱中所剩余的油量恰好相等，求两车的行驶速度．
相关试题
如图，∠MBN的两边BM，BN上分别有两点A、C，满足BC=2BA，作□ABCD，取AD的中点E，作CF⊥CD，CF与AB所在的直线交于点F。
（1）当∠B=
时，直接写出∠DEF的度数；
（2）在射线BM绕B点旋转的过程中，若∠B=
，∠DEF=
（
＜X＜
，＜Y＜），求：Y关于X的函数解析式及相应自变量X的取值范围，
已知，△ABC中，∠BAC=45°，以AB边为边以点B为直角顶点在△ABC外部作等腰直角三角形ABD，以AC边为斜边在△ABC外部作等腰直角三角形ACE，连结BE、DC，两条线段相交于F，试求∠EFC的度数．
（备用图）
已知：如图，四边形ABCD是关于坐标原点中心对称的四边形，其中点A
B
，反比例函数
经过点A．
（1）求反比例函数．
（2）设直线
经过C、D两点，在原有坐标系中画出并利用函数的图象，
直接写出不等式
的解集为：．
相关知识点
推荐套卷
粤公网安备 44130202000953号