某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛，他们取得的成绩(满分100分)的茎叶图如图所示，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.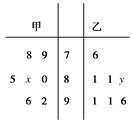
(1)求x和y的值；
(2)计算甲班七名学生成绩的方差．
的定义域为集合
，不等式
的解集为集合
．
，
．
．
的前n项和为构成数列
，数列
．若
，则
中，
分别是上、下底面的中心．已知
，
．
相关知识点
推荐套卷
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛，他们取得的成绩(满分100分)的茎叶图如图所示，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.
(1)求x和y的值；
(2)计算甲班七名学生成绩的方差．
粤公网安备 44130202000953号