某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3000名初中生、4000名高中生中作问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
(3)为了从4000份高中生的答卷中抽取一个容量为64的样本,如何使用系统抽样抽取到所需的样本?
相关知识点
推荐套卷
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其中左焦点F(﹣2,0).
,其中左焦点F(﹣2,0). ,数列
,数列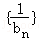 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.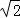 ,求椭圆C的方程;
,求椭圆C的方程; 粤公网安备 44130202000953号
粤公网安备 44130202000953号