已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程.
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求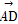
·
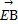的最小值.
的不等式
的解集为
，不等式
的解集为
．
，求实数
的取值范围； 
，求集合
且
，求实数
的取值范围．
是一个等差 数列，且
。
； （2）求
项和
的最大值。
的三个内角，他们的对边分别为a、b、c，且
。
求bc的值，并求
的最大值。
的解集。相关知识点
推荐套卷
已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程.
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求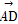·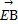的最小值.
粤公网安备 44130202000953号