已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.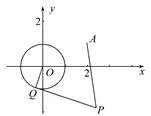
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
相关试题
为偶函数．
的值；
，当
时，求
的值域；
的最小值为1，
，
．
在
上不是单调函数，求实数
的取值范围．
，集合
．
；
．
的所有棱长都为2，
，平面
⊥平面
，
．
；
的平面角的余弦值；
上是否存在点
，使得
∥平面
，若存在求出
是边长为1的正方形，
⊥平面
⊥平面
；
，且二面角
的大小为
，求推荐套卷
已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
粤公网安备 44130202000953号