某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.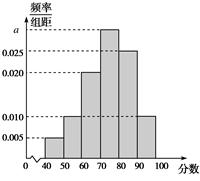
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
相关知识点
推荐套卷

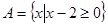 ,集合
,集合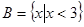 .
.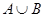 ;
;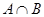 ;
;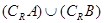
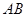 与
与 所成的角的大小是.
所成的角的大小是.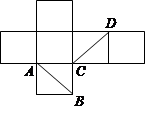
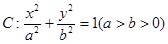 过点
过点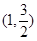 ,且离心率
,且离心率 .
.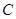 的标准方程;
的标准方程;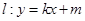 与椭圆
与椭圆 ,
, 两点(
两点(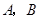 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为 ,且满足
,且满足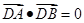 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
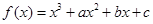 在
在 与
与 时都取得极值.
时都取得极值. 的值及
的值及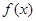 的极大值与极小值;
的极大值与极小值; 有三个互异的实根,求
有三个互异的实根,求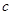 的取值范围;
的取值范围; ,不等式
,不等式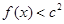 恒成立,求
恒成立,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号