亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部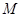 ,颖颖的头顶
,颖颖的头顶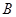 及亮亮的眼睛
及亮亮的眼睛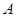 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置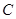 ,
,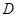 .然后测出两人之间的距离
.然后测出两人之间的距离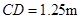 ,颖颖与楼之间的距离
,颖颖与楼之间的距离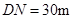 (
(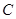 ,
,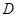 ,
,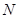 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高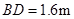 ,亮亮蹲地观测时眼睛到地面的距离
,亮亮蹲地观测时眼睛到地面的距离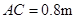 .你能根据以上测量数据帮助他们求出住宅楼的高度吗?
.你能根据以上测量数据帮助他们求出住宅楼的高度吗?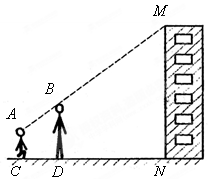
相关知识点
推荐套卷
亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部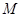 ,颖颖的头顶
,颖颖的头顶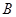 及亮亮的眼睛
及亮亮的眼睛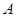 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置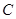 ,
,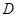 .然后测出两人之间的距离
.然后测出两人之间的距离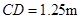 ,颖颖与楼之间的距离
,颖颖与楼之间的距离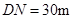 (
(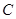 ,
,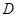 ,
,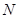 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高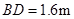 ,亮亮蹲地观测时眼睛到地面的距离
,亮亮蹲地观测时眼睛到地面的距离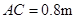 .你能根据以上测量数据帮助他们求出住宅楼的高度吗?
.你能根据以上测量数据帮助他们求出住宅楼的高度吗?