如图所示,已知在直角梯形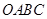 中,
中,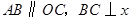 轴于点
轴于点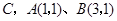 .动点
.动点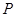 从
从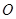 点出发,沿
点出发,沿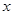 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过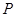 点作
点作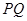 垂直于直线
垂直于直线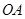 ,垂足为
,垂足为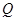 .设
.设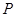 点移动的时间为
点移动的时间为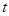 秒(
秒(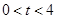 ),
), 与直角梯形
与直角梯形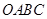 重叠部分的面积为
重叠部分的面积为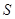 .
.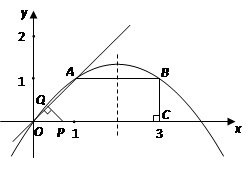
(1)求经过 三点的抛物线解析式;
三点的抛物线解析式;
(2)将 绕着点
绕着点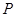 顺时针旋转
顺时针旋转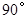 ,是否存在
,是否存在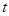 ,使得
,使得 的顶点
的顶点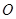 或
或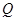 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出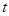 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)求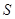 与
与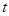 的函数关系式.
的函数关系式.
相关知识点
推荐套卷
如图所示,已知在直角梯形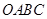 中,
中,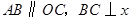 轴于点
轴于点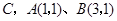 .动点
.动点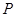 从
从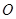 点出发,沿
点出发,沿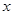 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过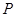 点作
点作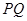 垂直于直线
垂直于直线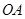 ,垂足为
,垂足为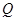 .设
.设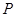 点移动的时间为
点移动的时间为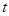 秒(
秒(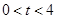 ),
), 与直角梯形
与直角梯形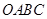 重叠部分的面积为
重叠部分的面积为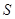 .
.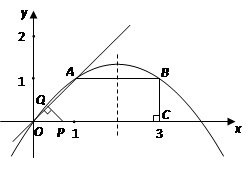
(1)求经过 三点的抛物线解析式;
三点的抛物线解析式;
(2)将 绕着点
绕着点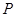 顺时针旋转
顺时针旋转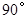 ,是否存在
,是否存在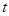 ,使得
,使得 的顶点
的顶点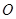 或
或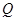 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出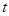 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)求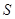 与
与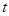 的函数关系式.
的函数关系式.