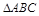与
在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标：
； 
；
；
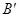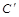⑵说明由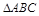经过怎样的平移得到 ．
⑶若点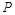
（
，
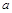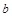）是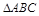内部一点，则平移后内的对应点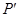
的坐标为 ；
⑷求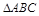的面积.
的整数解。
(1)作∠AOB角平分线(2)作线段AB垂直平分线
△DEF
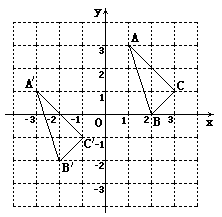
相关知识点
推荐套卷
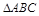与在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标： ； ； ；
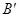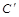⑵说明由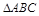经过怎样的平移得到 ．
⑶若点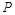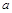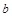（，）是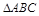内部一点，则平移后内的对应点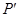的坐标为 ；
⑷求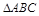的面积.
粤公网安备 44130202000953号