如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB= AB.直角梯形ACEF中,
AB.直角梯形ACEF中,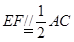 ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.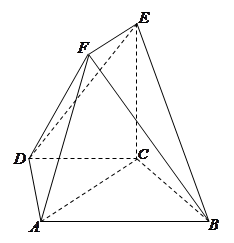
(1)求证: ;
;
(2)若直线DE与平面ACEF所成的角的正切值是 ,试求
,试求 的余弦值.
的余弦值.
推荐套卷
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB= AB.直角梯形ACEF中,
AB.直角梯形ACEF中,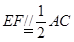 ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.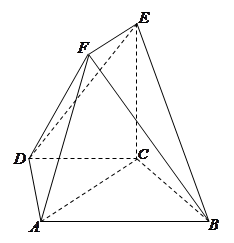
(1)求证: ;
;
(2)若直线DE与平面ACEF所成的角的正切值是 ,试求
,试求 的余弦值.
的余弦值.