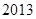 年
年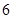 月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为
月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为 、
、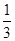 、
、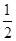 、
、 ,并且各个环节的直播收看互不影响.
,并且各个环节的直播收看互不影响.
(1)现有该班甲、乙、丙三名同学,求这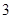 名同学至少有
名同学至少有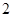 名同学收看发射直播的概率;
名同学收看发射直播的概率;
(2)若用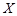 表示该班某一位同学收看的环节数,求
表示该班某一位同学收看的环节数,求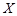 的分布列与期望.
的分布列与期望.
推荐套卷
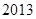 年
年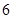 月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为
月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为 、
、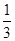 、
、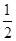 、
、 ,并且各个环节的直播收看互不影响.
,并且各个环节的直播收看互不影响.
(1)现有该班甲、乙、丙三名同学,求这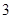 名同学至少有
名同学至少有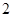 名同学收看发射直播的概率;
名同学收看发射直播的概率;
(2)若用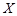 表示该班某一位同学收看的环节数,求
表示该班某一位同学收看的环节数,求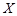 的分布列与期望.
的分布列与期望.