设数列{an}：1，－2，－2,3,3,3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)k－1k，…，即当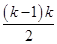
<n≤
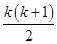(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)．对于l∈N*，定义集合Pl＝{n|Sn是an的整数倍，n∈N*，且1≤n≤l}．
(1)求集合P11中元素的个数；
(2)求集合P2 000中元素的个数．
的函数
是奇函数。
的值；
，不等式
恒成立，求
的取值范围；
，若
在
上的最大值为
，求
.
是增函数.
的值
，若
，求实数
的值推荐套卷
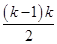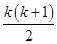设数列{an}：1，－2，－2,3,3,3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)k－1k，…，即当<n≤(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)．对于l∈N*，定义集合Pl＝{n|Sn是an的整数倍，n∈N*，且1≤n≤l}．
(1)求集合P11中元素的个数；
(2)求集合P2 000中元素的个数．
粤公网安备 44130202000953号