某地最近十年粮食需求量逐年上升，下表是部分统计数据：
| 年份 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
| 需求量（万吨） |
3 |
6 |
5 |
7 |
8 |
（1）利用所给数据求年需求量与年份之间的回归直线方程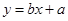
；
（2）利用（1）中所求出的直线方程预测该地第6年的粮食需求量．
内有一点
，
把角分成
两个角，且
求△
（
右支上的一点，
,
分别是左右焦点，且焦距为2
，求△P
到110
，
的最小值为
，求
的值推荐套卷
某地最近十年粮食需求量逐年上升，下表是部分统计数据：
| 年份 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
| 需求量（万吨） |
3 |
6 |
5 |
7 |
8 |
（1）利用所给数据求年需求量与年份之间的回归直线方程；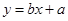
（2）利用（1）中所求出的直线方程预测该地第6年的粮食需求量．
粤公网安备 44130202000953号