调查某市出租车使用年限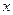
和该年支出维修费用
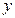（万元），得到数据如下：
| 使用年限 |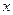
2 |
3 |
4 |
5 |
6 |
| 维修费用 |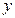
2．2 |
3．8 |
5．5 |
6．5 |
7．0 |
（1） 求线性回归方程；
（2）由（1）中结论预测第10年所支出的维修费用．（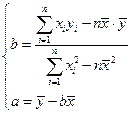
）
相关试题
在区间
上都
有意义，且在此区间上
为增函数，
；
为减函数，
.
在
的单调性，并给出证明.
，推荐套卷
调查某市出租车使用年限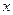和该年支出维修费用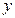（万元），得到数据如下：
| 使用年限 |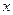
2 |
3 |
4 |
5 |
6 |
| 维修费用 |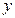
2．2 |
3．8 |
5．5 |
6．5 |
7．0 |
（1） 求线性回归方程；
（2）由（1）中结论预测第10年所支出的维修费用．（）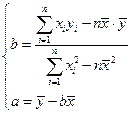
粤公网安备 44130202000953号