为拉动经济增长，某市决定新建一批基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目个数分别占总数的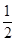
，
，
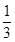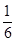，现在3名工人独立地从中任意一个项目参与建设．
(1)求他们选择的项目所属类别互不相同的概率．
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数，求X的分布列及数学期望．
相关试题
.
对任意实数
恒成立，求实数
的取值范围；
，解不等式
.
的各项均为正数，它的前
项的和为
，且
，数列
满足
．其中
．
，求证：数列
的前
（
．
的最小值，及取最小值时
的值；
的内角
的对边分别为
且
，
，若
，求
的值．
的公差
，该数列的前
项和为
，且满足
．
，
，求数列
的通项公式．
的棱长为
，
分别是棱
的中点，
的体积.
推荐套卷
为拉动经济增长，某市决定新建一批基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目个数分别占总数的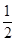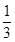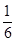，，，现在3名工人独立地从中任意一个项目参与建设．
(1)求他们选择的项目所属类别互不相同的概率．
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数，求X的分布列及数学期望．
粤公网安备 44130202000953号