如图，在四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC于E，AF⊥DF于F，△BEA旋转后能与△DFA重叠．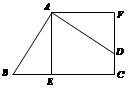
⑴△BEA绕_______点________时针方向旋转_______度能与△DFA重合；
⑵若AE＝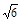
cm，求四边形AECF的面积．
的值与字母x的取值无关，求
的值。
，其中a=-2，b=3.
，
，﹣（﹣1）100，﹣22．推荐套卷
如图，在四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC于E，AF⊥DF于F，△BEA旋转后能与△DFA重叠．
⑴△BEA绕_______点________时针方向旋转_______度能与△DFA重合；
⑵若AE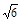＝cm，求四边形AECF的面积．
粤公网安备 44130202000953号