已知函数f(x)＝－x3＋x2，g(x)＝aln x，a∈R.
(1)若对任意x∈[1，e]，都有g(x)≥－x2＋(a＋2)x恒成立，求a的取值范围；
(2)设F(x)＝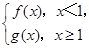
若P是曲线y＝F(x)上异于原点O的任意一点，在曲线y＝F(x)上总存在另一点Q，使得△POQ中的∠POQ为钝角，且PQ的中点在y轴上，求a的取值范围．
相关试题
在
与
时都取得极值．
的值；
，不等式
恒成立，求
的取值范围．
是公差不为0的等差数列，
，且
，
，
成等比数列．
，求数列
的前
项和
．
，求证: 
的最小值及对应的x、y值．
满足
， 
的最大值及对应的x、y、z值．
．
．
推荐套卷
已知函数f(x)＝－x3＋x2，g(x)＝aln x，a∈R.
(1)若对任意x∈[1，e]，都有g(x)≥－x2＋(a＋2)x恒成立，求a的取值范围；
(2)设F(x)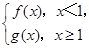＝若P是曲线y＝F(x)上异于原点O的任意一点，在曲线y＝F(x)上总存在另一点Q，使得△POQ中的∠POQ为钝角，且PQ的中点在y轴上，求a的取值范围．
粤公网安备 44130202000953号