2013年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
(2)若2013年北京市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
相关知识点
推荐套卷
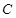 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为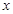 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线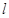 的参数方程是
的参数方程是 参数),点
参数),点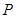 是曲线
是曲线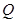 是直线
是直线 |的最小值.
|的最小值.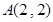 在矩阵
在矩阵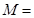
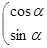
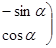 对应变换的作用下得到的点为
对应变换的作用下得到的点为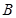
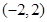 ,求矩阵
,求矩阵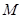 的逆矩阵.
的逆矩阵.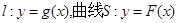 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.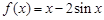 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”. 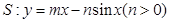 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明. :
: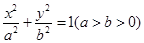 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形. (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线 交椭圆
交椭圆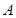 、
、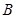 两点,设点
两点,设点 轴的对称点为
轴的对称点为 .
.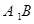 过
过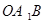 面积的取值范围.
面积的取值范围.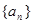 中,其前
中,其前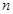 项和
项和 与
与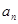 满足关系式:
满足关系式: 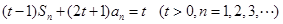 .
.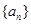 的公比为
的公比为 ,已知数列
,已知数列 ,
,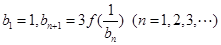 ,求
,求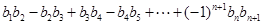 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号