矩形 的中心在坐标原点,边
的中心在坐标原点,边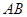 与
与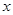 轴平行,
轴平行,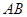 =8,
=8, =6.
=6.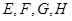 分别是矩形四条边的中点,
分别是矩形四条边的中点,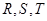 是线段
是线段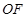 的四等分点,
的四等分点,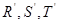 是线段
是线段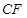 的四等分点.设直线
的四等分点.设直线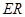 与
与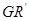 ,
,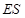 与
与 ,
, 与
与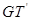 的交点依次为
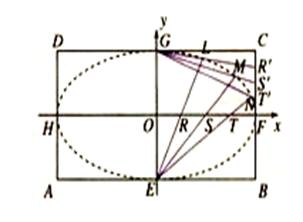
的交点依次为 .
.
(1)求以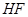 为长轴,以
为长轴,以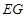 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段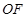 的
的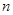 (
(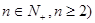 等分点从左向右依次为
等分点从左向右依次为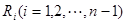 ,线段
,线段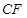 的
的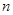 等分点从上向下依次为
等分点从上向下依次为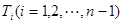 ,那么直线
,那么直线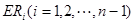 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
推荐套卷
矩形 的中心在坐标原点,边
的中心在坐标原点,边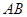 与
与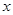 轴平行,
轴平行,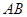 =8,
=8, =6.
=6.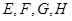 分别是矩形四条边的中点,
分别是矩形四条边的中点,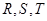 是线段
是线段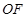 的四等分点,
的四等分点,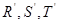 是线段
是线段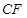 的四等分点.设直线
的四等分点.设直线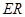 与
与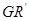 ,
,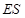 与
与 ,
, 与
与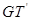 的交点依次为
的交点依次为 .
.
(1)求以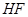 为长轴,以
为长轴,以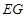 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段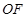 的
的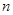 (
(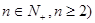 等分点从左向右依次为
等分点从左向右依次为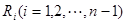 ,线段
,线段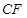 的
的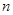 等分点从上向下依次为
等分点从上向下依次为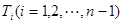 ,那么直线
,那么直线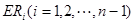 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)