某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为 万元,年维修费用第一年是
万元,年维修费用第一年是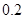 万元,第二年是
万元,第二年是 万元,第三年是
万元,第三年是 万元,…,以后逐年递增
万元,…,以后逐年递增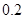 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用 年的维修费用的和为
年的维修费用的和为 ,年平均费用为
,年平均费用为 .
.
(1)求出函数 ,
, 的解析式;
的解析式;
(2)这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
推荐套卷
某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为 万元,年维修费用第一年是
万元,年维修费用第一年是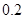 万元,第二年是
万元,第二年是 万元,第三年是
万元,第三年是 万元,…,以后逐年递增
万元,…,以后逐年递增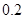 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用 年的维修费用的和为
年的维修费用的和为 ,年平均费用为
,年平均费用为 .
.
(1)求出函数 ,
, 的解析式;
的解析式;
(2)这种汽车使用多少年时,它的年平均费用最小?最小值是多少?