为贯彻“激情工作,快乐生活”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数为X,试写出X的分布列,并求X的数学期望.
相关知识点
推荐套卷
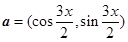 ,
,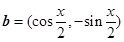 ,且
,且 ,
, (
(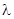 为常数),求:
为常数),求: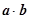 及
及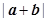 ;
;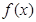 的最小值是
的最小值是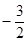 ,求实数
,求实数 ,
,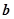 ,
, 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
. ,且
,且 ,求
,求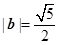 ,且
,且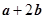 与
与 垂直,求
垂直,求 .
. (
( ,
, )为偶函数,其图象上相邻的两个最高点之间的距离为
)为偶函数,其图象上相邻的两个最高点之间的距离为 .
. 的解析式;(2)若
的解析式;(2)若 ,
, ,求
,求 的值.
的值. ,求函数在区间
,求函数在区间 上的单调增区间;
上的单调增区间; .
. ,
, .
. 的最小正周期;(2)求
的最小正周期;(2)求 ,求
,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号