在等腰梯形ABCD中，AD∥BC，AD＝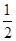
BC，∠ABC＝60°，N是BC的中点，将梯形ABCD绕AB旋转90°，得到梯形ABC′D′(如图)．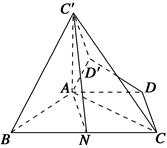
(1)求证：AC⊥平面ABC′；
(2)求证：C′N∥平面ADD′；
(3)求二面角A-C′N-C的余弦值．
相关试题
与直线
相交于点P，
平行的直线方程；
中，已知
，
，
； 
，求数列
前5项的和
.
的值；
的最大值和最小值推荐套卷
在等腰梯形ABCD中，AD∥BC，AD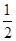＝BC，∠ABC＝60°，N是BC的中点，将梯形ABCD绕AB旋转90°，得到梯形ABC′D′(如图)．
(1)求证：AC⊥平面ABC′；
(2)求证：C′N∥平面ADD′；
(3)求二面角A-C′N-C的余弦值．
粤公网安备 44130202000953号