（1）已知函数f(x)＝ex－1－tx，∃x0∈R，使f(x0)≤0，求实数t的取值范围；
（2）证明：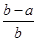
＜ln
＜
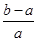，其中0＜a＜b；
（3）设[x]表示不超过x的最大整数，证明：[ln(1＋n)]≤[1＋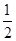
＋ ＋
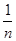]≤1＋[lnn]（n∈N*）．
的前
项的和
是数列
的图象与
轴交于
的充要条件为
．
，命题
，若
是
的必要条件，求实数
的取值范围．
至少有一个负根的充要条件．
是
的充分条件．推荐套卷
（1）已知函数f(x)＝ex－1－tx，∃x0∈R，使f(x0)≤0，求实数t的取值范围；
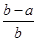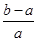（2）证明：＜ln＜，其中0＜a＜b；
（3）设[x]表示不超过x的最大整数，证明：[ln(1＋n)]≤[1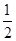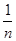＋＋ ＋]≤1＋[lnn]（n∈N*）．
粤公网安备 44130202000953号