如图,椭圆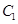 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在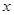 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆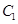 的长轴长为
的长轴长为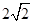 ,且椭圆
,且椭圆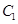 的左准线
的左准线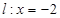 被椭圆
被椭圆 截得的线段
截得的线段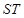 长为
长为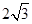 ,已知点
,已知点 是椭圆
是椭圆 上的一个动点.
上的一个动点.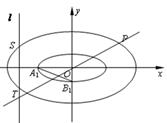
⑴求椭圆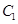 与椭圆
与椭圆 的方程;
的方程;
⑵设点 为椭圆
为椭圆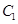 的左顶点,点
的左顶点,点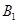 为椭圆
为椭圆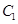 的下顶点,若直线
的下顶点,若直线 刚好平分
刚好平分 ,求点
,求点 的坐标;
的坐标;
⑶若点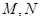 在椭圆
在椭圆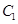 上,点
上,点 满足
满足 ,则直线
,则直线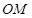 与直线
与直线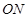 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
推荐套卷
如图,椭圆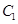 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在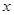 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆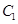 的长轴长为
的长轴长为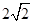 ,且椭圆
,且椭圆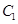 的左准线
的左准线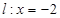 被椭圆
被椭圆 截得的线段
截得的线段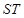 长为
长为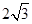 ,已知点
,已知点 是椭圆
是椭圆 上的一个动点.
上的一个动点.
⑴求椭圆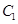 与椭圆
与椭圆 的方程;
的方程;
⑵设点 为椭圆
为椭圆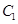 的左顶点,点
的左顶点,点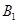 为椭圆
为椭圆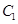 的下顶点,若直线
的下顶点,若直线 刚好平分
刚好平分 ,求点
,求点 的坐标;
的坐标;
⑶若点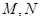 在椭圆
在椭圆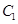 上,点
上,点 满足
满足 ,则直线
,则直线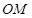 与直线
与直线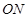 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.