在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为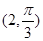
．
(1)求圆C的极坐标方程；
(2)在以极点O为原点，以极轴为x轴正半轴建立的直角坐标系中，直线
的参数方程为
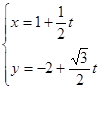（t为参数），直线与圆C相交于A，B两点，已知定点
,求|MA|·|MB|．
相关试题
为正方形，
平面
且垂直于
的平面分别交
，
于
，
，
．求证：
．
中，
，
，
，
分别是
，
，
，
的中点．求证：四边形
是平行四边形．
中，
，
，
分别是
上的动点，
．
为何值，总有平面
；
？
表示为
的函数．
cm、
cm，侧棱长为推荐套卷
在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为．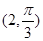
(1)求圆C的极坐标方程；
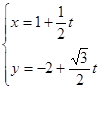(2)在以极点O为原点，以极轴为x轴正半轴建立的直角坐标系中，直线的参数方程为（t为参数），直线与圆C相交于A，B两点，已知定点,求|MA|·|MB|．
粤公网安备 44130202000953号