已知平行四边形ABCD中,对角线AC和BD相交于点O,AC=10,BD=8.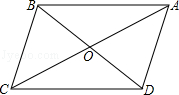
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积;
(3)试讨论:若把题目中“平行四边形ABCD”改为“四边形ABCD”,且∠AOD=θ,AC=a,BD=b,试求四边形ABCD的面积(用含θ,a,b的代数式表示).
推荐套卷
已知平行四边形ABCD中,对角线AC和BD相交于点O,AC=10,BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积;
(3)试讨论:若把题目中“平行四边形ABCD”改为“四边形ABCD”,且∠AOD=θ,AC=a,BD=b,试求四边形ABCD的面积(用含θ,a,b的代数式表示).