已知正项数列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的两个实根.
1)x+bn=0的两个实根.
(1)求a2,b1;
(2)求数列{an}的通项公式;
(3)若 ,
, 是
是 前
前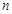 项和,
项和,  ,当
,当 时,试比较
时,试比较 与
与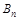 的大小.
的大小.
相关知识点
推荐套卷
已知正项数列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的两个实根.
1)x+bn=0的两个实根.
(1)求a2,b1;
(2)求数列{an}的通项公式;
(3)若 ,
, 是
是 前
前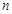 项和,
项和,  ,当
,当 时,试比较
时,试比较 与
与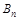 的大小.
的大小.