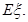盒子中装有四张大小形状均相同的卡片，卡片上分别标有数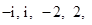
其中
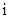是虚数单位．称“从盒中随机抽取一张，记下卡片上的数后并放回”为一次试验（设每次试验的结果互不影响）．
（1）求事件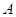
“在一次试验中，得到的数为虚数”的概率
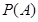与事件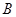
“在四次试验中，
至少有两次得到虚数” 的概率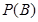
；
（2）在两次试验中，记两次得到的数分别为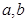
，求随机变量
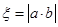的分布列与数学期望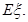
相关试题
，函数
．
有极大值32，求实数
的值；
，不等式
恒成立，求实数
， 
在
处有极值，求
；（2）若
上为增函数，求
，直线x+y=3以及两坐标轴所围成的图形的面积S.
推荐套卷
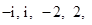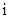盒子中装有四张大小形状均相同的卡片，卡片上分别标有数其中是虚数单位．称“从盒中随机抽取一张，记下卡片上的数后并放回”为一次试验（设每次试验的结果互不影响）．
（1）求事件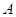 “在一次试验中，得到的数为虚数”的概率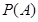与事件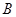 “在四次试验中，
至少有两次得到虚数” 的概率；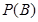
（2）在两次试验中，记两次得到的数分别为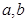，求随机变量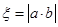的分布列与数学期望
粤公网安备 44130202000953号