中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后
驾车和醉酒驾车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布
直方图.
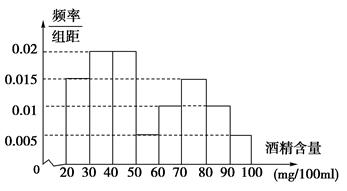
(1)根据频率分布直方图,求此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.