城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的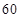 名候车乘客中随机抽取
名候车乘客中随机抽取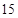 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成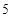 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 |
候车时间 |
人数 |
| 一 |
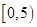 |
 |
| 二 |
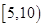 |
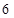 |
| 三 |
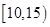 |
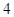 |
| 四 |
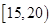 |
 |
| 五 |
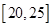 |
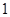 |
(1)求这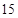 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这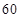 名乘客中候车时间少于
名乘客中候车时间少于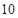 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的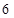 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
相关知识点
推荐套卷
 是椭圆
是椭圆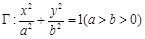 的左右焦点,椭圆
的左右焦点,椭圆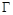 的离心率
的离心率 ,
, 是
是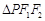 的面积的最大值为1.
的面积的最大值为1.
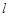 是椭圆在点P处的切线,过
是椭圆在点P处的切线,过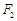 作
作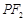 的垂线,交直线
的垂线,交直线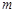 上,并求直线
上,并求直线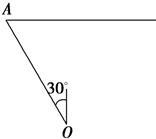
 ,设不等式组
,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记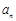 (横、纵坐标均为整数的点称为整点).
(横、纵坐标均为整数的点称为整点).
 的值的规律,求
的值的规律,求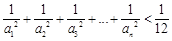 .
. ,设函数
,设函数 .
.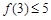 ,求a的取值范围.
,求a的取值范围.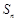 是数列
是数列 的前n项和,满足
的前n项和,满足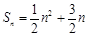 ,正项等比数列
,正项等比数列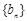 的前n项和为
的前n项和为 ,且满足
,且满足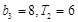 .
. ,求数列{cn}的前n项和
,求数列{cn}的前n项和 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号