端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量特设计了一个游戏,其规则是：分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等（若指针恰好落在分界线上重转）,当两个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.
（1）用树状图或列表的方法（只选其中一种）表示出游戏可能出现的所有结果.
（2）若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少？
相关试题
，
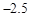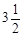，0，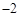
，
，
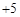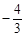，并按从小到大的顺序用“＜”连接起来。把下列各数分别填在表示它所在的集合里：
，
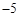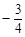，0，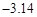
，
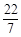，2012，1.99，
，
（1）正数集合：{}；
（2）负数集合：{}；
（3）整数集合：{}；
（4）分数集合：{}。
.小明用一根铁丝围成了一个面积为25cm2的正方形，小颖对小明说：“我用这根铁丝可以围个面积也是25cm2的圆，且铁丝还有剩余”。问小颖能成功吗？若能，请估计可剩多少厘米的铁丝？（误差小于1cm）若不能，请说明理由。
，
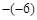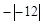
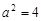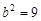，且ab＜0，求
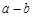的值。相关知识点
推荐套卷
粤公网安备 44130202000953号