首页 组卷 试卷 教案 课件 作文 范文 模板 中考 高考
  首页 / 初中数学 / 试题详细
  • 更新 2022-09-03
  • 科目 数学
  • 题型 解答题
  • 难度 中等
  • 浏览 1315
挑错有奖

如图，一架长2.5米的梯子AB斜靠在竖直的墙AC上，这时B到墙AC的距离为0.7米．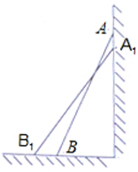

（1）若梯子的顶端A沿墙AC下滑0.9米至A1处，求点B向外移动的距离BB1的长；
（2）若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半，试求梯子沿墙AC下滑的距离是多少米？

登录免费查看答案和解析
相关试题

已知:如图5-，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DEF的平分线相交于点P.求证∠P=90°.

  • 题型：未知
  • 难度：未知
收藏 答案/解析

如图所示,请写出能够得到直线AB∥CD的所有直接条件.

  • 题型：未知
  • 难度：未知
收藏 答案/解析

如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?

  • 题型：未知
  • 难度：未知
收藏 答案/解析

如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E=30°,试说明AB∥CD.

  • 题型：未知
  • 难度：未知
收藏 答案/解析

如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.

  • 题型：未知
  • 难度：未知
收藏 答案/解析
相关知识点
一元二次方程的最值
推荐套卷
热门套卷

如图，一架长2.5米的梯子AB斜靠在竖直的墙AC上，这时B到

帮助中心 启点学教育 优题课 范文网 作文网 关于我们 联系我们 侵权举报
粤ICP备20024846号     粤公网安备 粤公网安备 44130202000953号
Copyright ©2020-2026 优题课 youtike.com 版权所有     Powered by：Youtike Platform 6.8.11
声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或 联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。