甲、乙两名同学玩抽纸牌比大小的游戏,规则是:“甲将同一副牌中正面分别标有数字1,3,6的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;乙将同一副牌中正面分别标有数字2,3,4的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;若甲同学抽得的数字比乙同学抽得的数字大,甲获胜,反之乙获胜,若数字相同,视为平局.”
(1)请用画树状图或列表的方法计算出平局的概率;
(2)说明这个规则对甲、乙双方是否公平.
相关知识点
推荐套卷
 的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端
的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端 的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端
的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端 ,台阶AC的坡度为
,台阶AC的坡度为 (即
(即 ),且
),且 、
、 、
、 三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°
三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65° 2.1,cos65°
2.1,cos65° 1.7,结果保留一位小数).
1.7,结果保留一位小数).
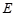 、
、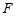 是
是 、
、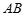 的中点,
的中点,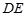 、
、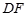 的延长线分别交
的延长线分别交 的延长线于
的延长线于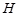 、
、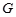 ;
;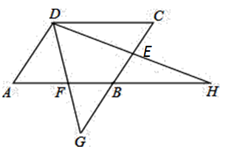
 为菱形,试判断
为菱形,试判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.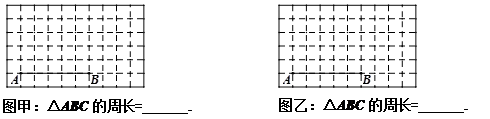
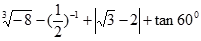 ;
;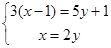
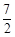 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).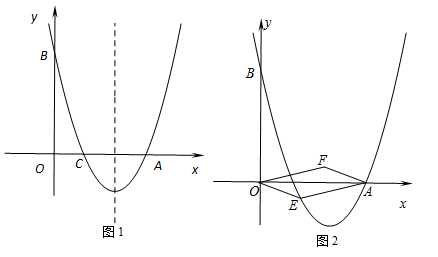
 粤公网安备 44130202000953号
粤公网安备 44130202000953号