已知坐标平面内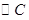 :
: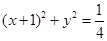 ,
, :
: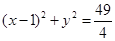 .动点P与
.动点P与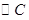 外切与
外切与 内切.
内切.
(1)求动圆心P的轨迹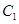 的方程;
的方程;
(2)若过D点的斜率为2的直线与曲线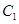 交于两点A、B,求AB的长;
交于两点A、B,求AB的长;
(3)过D的动直线与曲线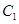 交于A、B两点,线段中点为M,求M的轨迹方程.
交于A、B两点,线段中点为M,求M的轨迹方程.
推荐套卷
已知坐标平面内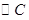 :
: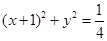 ,
, :
: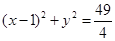 .动点P与
.动点P与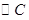 外切与
外切与 内切.
内切.
(1)求动圆心P的轨迹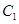 的方程;
的方程;
(2)若过D点的斜率为2的直线与曲线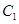 交于两点A、B,求AB的长;
交于两点A、B,求AB的长;
(3)过D的动直线与曲线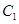 交于A、B两点,线段中点为M,求M的轨迹方程.
交于A、B两点,线段中点为M,求M的轨迹方程.