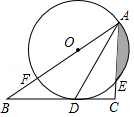
（1）如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 ．
（2）如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由．
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由．
相关试题
如图：AD平分∠CAB，过D作DM⊥AC于M，DN⊥AB于N，∠ACD+∠DBA=1800，AC=9，AB=21，BD=10．
求：（1）CD的长；
（2）求AD的长．
如图，已知△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D．
（1）直线BE与AD的位置关系是 ；BE与AD之间的距离是线段 的长；
（2） 若AD＝6cm，BE＝2cm．，求BE与AD之间的距离．
如图， ∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线，为什么?
相关知识点
推荐套卷
粤公网安备 44130202000953号