已知函数f(x)=x3+ax-2,(a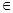
R).
(l)若f(x)在区间(1,+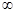
)上是增函数，求实数a的取值范围;
(2)若
，且f(x0)=3，求x0的值；
(3)若
，且在R上是减函数，求实数a的取值范围。
对应的变换作用下得到的图形．
在矩阵
作用下变换所得的图形对应的曲线方程．
之下的对应点的坐标为(－2，－4)，求m、k的值．
对应的变换作用下得到的点的坐标．相关知识点
推荐套卷
已知函数f(x)=x3+ax-2,(a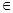R).
(l)若f(x)在区间(1,+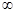)上是增函数，求实数a的取值范围;
(2)若，且f(x0)=3，求x0的值；
(3)若，且在R上是减函数，求实数a的取值范围。
粤公网安备 44130202000953号