已知圆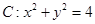
，直线
，以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系.
（1）将圆C和直线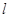
方程化为极坐标方程；
（2）P是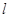上的点，射线OP交圆C于点R，又点Q在OP上且满足
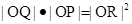，当点P在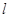上移动时，求点Q轨迹的极坐标方程.
相关试题
的图象与
轴的交点为
，它在
和
．
的解析式；
满足
，求
的值．
，
时，求
的取值集合；
的单调递增区间 .在△ABC中, 若I是△ABC的内心, AI的延长线交BC于D, 则有
称之为三角形的内角平分线定理, 现已知AC＝2, BC＝3, AB＝4, 且
, 求实数
及
的值.
满足
，
与向量
的夹角为钝角，求实数t的取值范围.
的最大值及相对应的
的值.推荐套卷
已知圆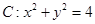，直线，以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系.
（1）将圆C和直线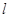方程化为极坐标方程；
（2）P是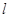上的点，射线OP交圆C于点R，又点Q在OP上且满足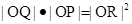，当点P在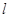上移动时，求点Q轨迹的极坐标方程.
在△ABC中, 若I是△ABC的内心, AI的延长线交BC于D, 则有称之为三角形的内角平分线定理, 现已知AC＝2, BC＝3, AB＝4, 且, 求实数及的值.
粤公网安备 44130202000953号