已知函数 为奇函数.
为奇函数.
(1)求常数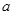 的值;
的值;
(2)判断函数的单调性,并说明理由;
(3)函数 的图象由函数
的图象由函数 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出 的一个对称中心,若
的一个对称中心,若 ,求
,求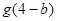 的值.
的值.
相关知识点
推荐套卷
已知函数 为奇函数.
为奇函数.
(1)求常数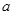 的值;
的值;
(2)判断函数的单调性,并说明理由;
(3)函数 的图象由函数
的图象由函数 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出 的一个对称中心,若
的一个对称中心,若 ,求
,求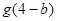 的值.
的值.